| 연산자 | 표현 | 입력값 | 결과값 | 의미 |
| gradient | 스칼라 | 벡터 | 기울기 | |
| divergence | 벡터 | 스칼라 | 발산 | |
| curl | 벡터 | 벡터 | 회전 |
[1] https://e-magnetica.pl/doku.php/vector_calculus
아래의 그림은 스칼라의 gradient와 벡터의 divergence, curl 연산과의 관계를 잘 보여줍니다.

아래는 gradient와 divergence, curl을 그래픽적으로 가장 잘 보여준 그림입니다.

1. Gradient: 스칼라 장의 x, y, z방향 기울기 벡터
gradient는 입력이 스칼라이고, 계산된 결과 값이 벡터입니다.
물리적인 의미는 스칼라장의 기울기(경사)를 나타냅니다.
gradient가 0이면 기울기가 0이되고, 0보다 크면 기울기가 상승, 0보다 작으면 벡터장의 기울기가 감소함을 의미합니다.
2. Divergence: 벡터장의 x, y, z방향 기울기 성분합
divergence는 입력은 벡터, 계산된 값은 스칼라입니다.
의미는 벡터장의 발산정도를 나타냅니다.
divergence값이 0이면 벡터장의 입출입이 같아 발산이 없으며, 0보다 크면 벡터장이 밖으로 발산되며, 0보다 작으면 벡터장이 안으로 수렴하는 것을 의미합니다.
3. Curl: 벡터장의 회전
curl은 입력도 벡터, 출력도 벡터가 됩니다.
물리적 의미는 벡터장의 회전을 의미합니다.
curl 값이 0보다 크면 해당 평면에 대해 반시계방향(CCW)회전, 0보다 작으면 시계방향(CW) 방향으로 회전, 0이면 회전이 없습니다.
간단한 예를 들어서 설명을 해보면, 아래는 각 스칼라장

각 스칼라장
세 벡터장 모두 curl의 값은 0이 되고,
회전을 보여주기 위해 다른 예를 들어보겠습니다.
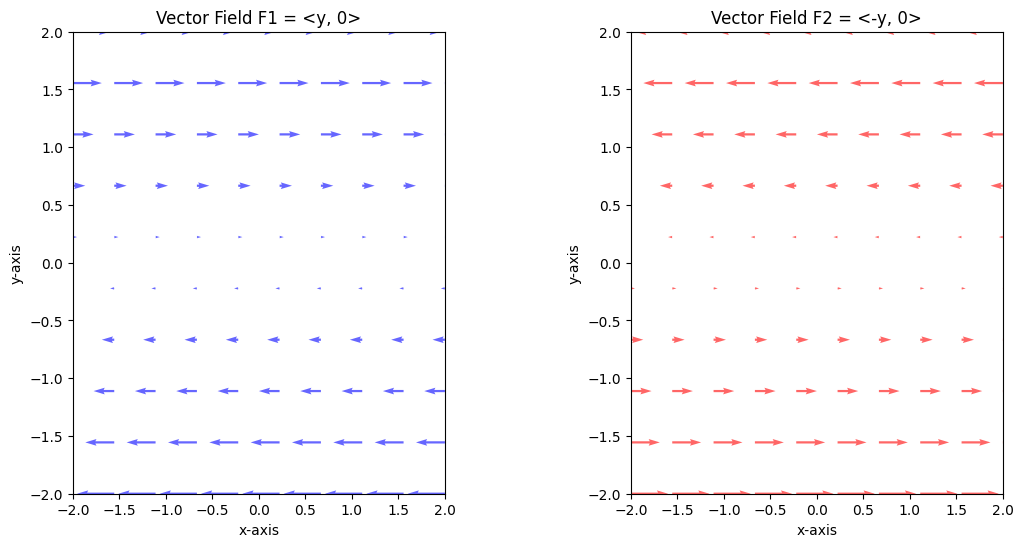
각 벡터장 F에 대해서 divergence와 curl을 구하면, 이번에는 divergence는 모두 0입니다. 이는 벡터장 안으로 유입되는 양과 유출되는 양이 동일함을 의미합니다.
curl의 경우, 첫 번째 벡터장의 경우 0보다 작습니다. 이는 벡터장이 시계방향으로 회전함을 의미합니다.
두 번째 벡터장의 경우 curl의 값이 0보다 큽니다. 이는 벡터장의 반시계방향 회전을 의미합니다.
위 두 벡터장의 경우, 각 벡터장을 gradient 결과로 가지는 스칼라장
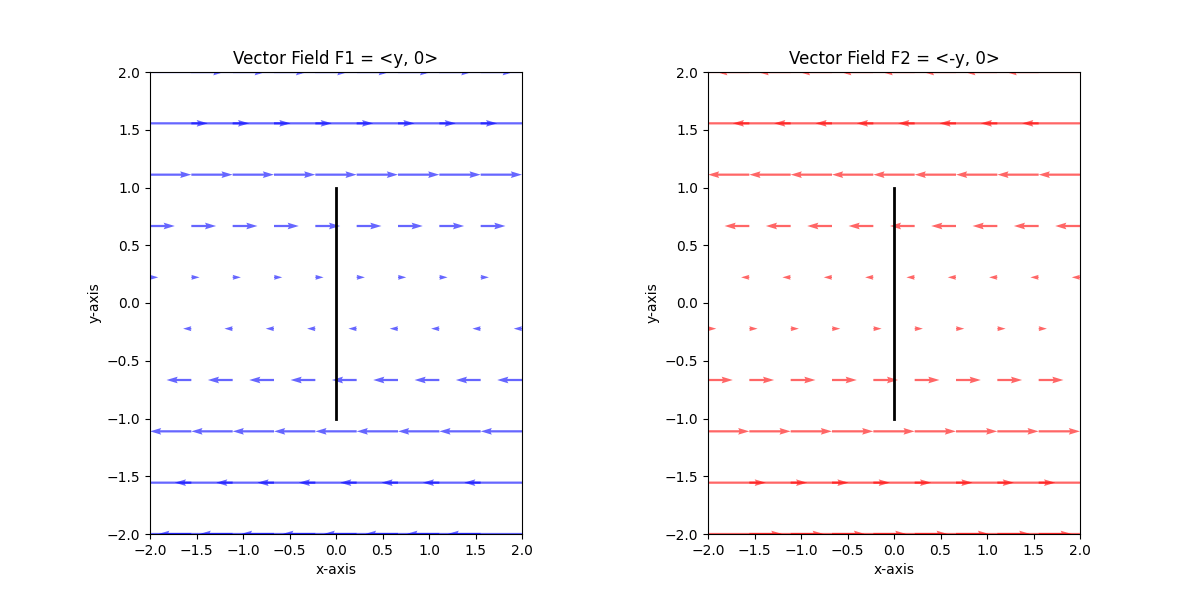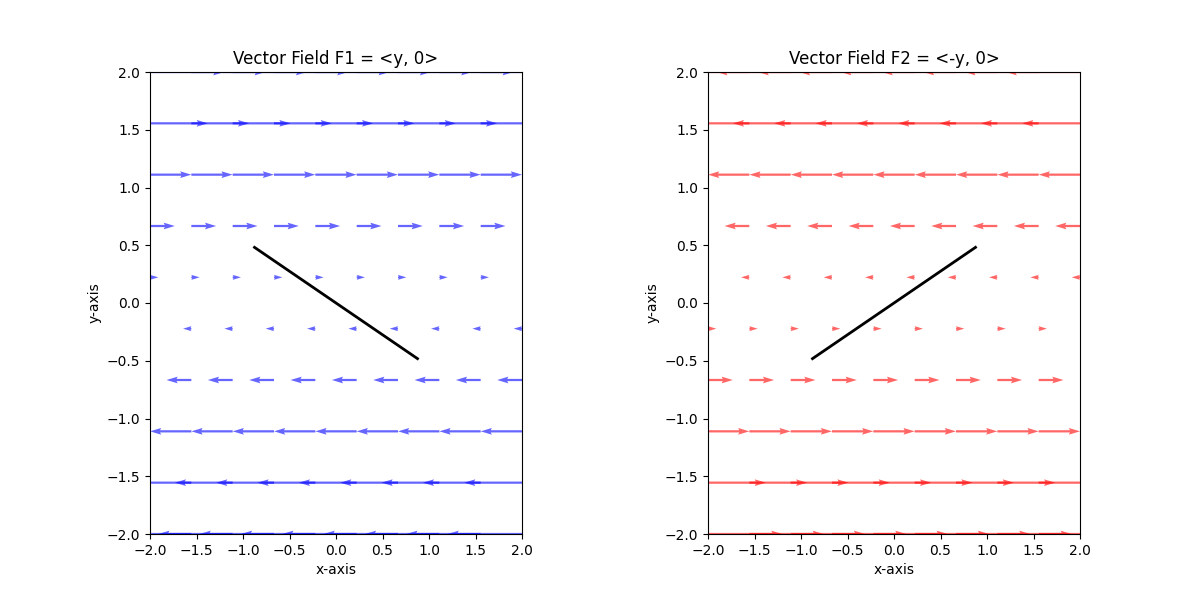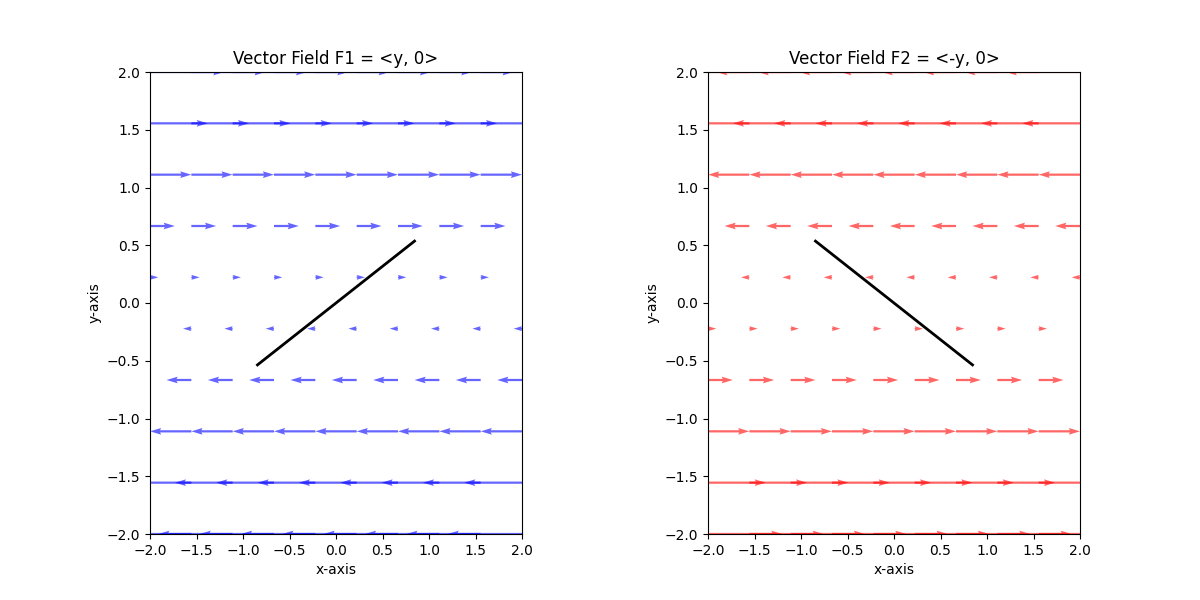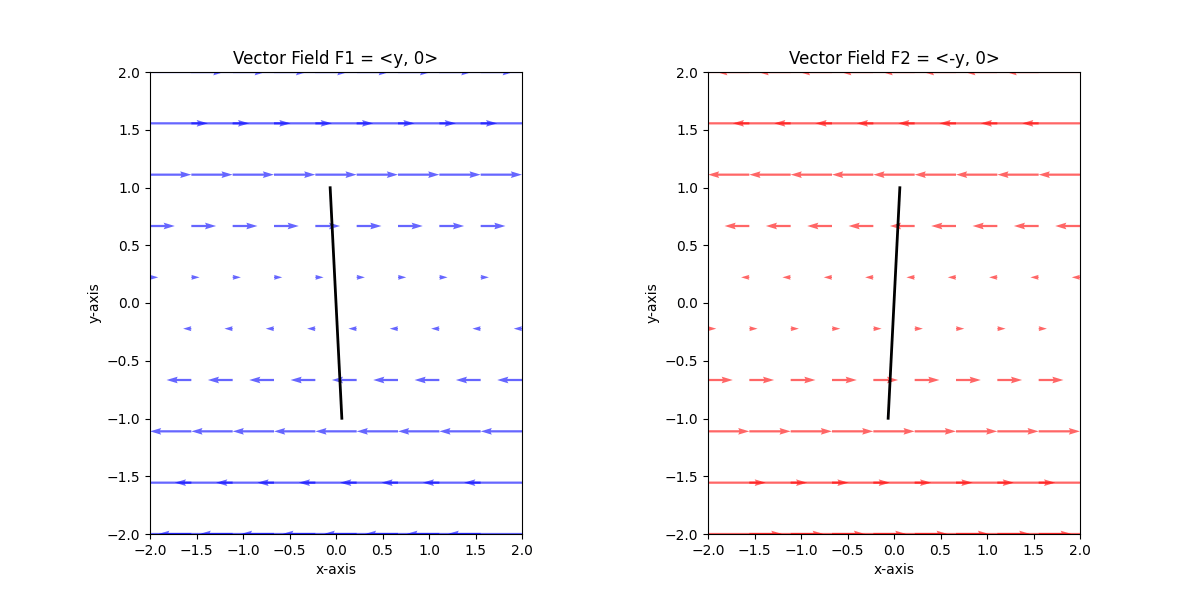
각 벡터장의 임의에 위치에 막대기를 위치시킨다면, 아래와 같이 회전할 것입니다. 이는 벡터장의 curl에 대해서 이해를 돕는데 아주 좋은 방법입니다.
[1] https://e-magnetica.pl/doku.php/vector_calculus
[2] https://x.com/CalcInsights_/status/1865443455075541077
[3] https://medium.com/@prmj2187/understanding-divergence-and-curl-through-vector-fields-449c43a6806b
[4] https://www.youtube.com/watch?v=rB83DpBJQsE&ab_channel=3Blue1Brown
'자격증.hack > 공학기초' 카테고리의 다른 글
| 텐서 표기법(Indicial notation) (0) | 2025.01.26 |
|---|---|
| 그린의 정리, 2차원 발산정리 (스토크스의 정리, 가우스의 발산정리) (0) | 2025.01.15 |
| 불확실성 전파(Propagation of uncertainty) = 불확도 전파 (0) | 2025.01.08 |
| 일반화된 연속방정식 유도 (레이놀즈 수송정리) (1) | 2025.01.05 |
| 베르누이 방정식(Bernoulli's equation) 유도 (0) | 2025.01.02 |