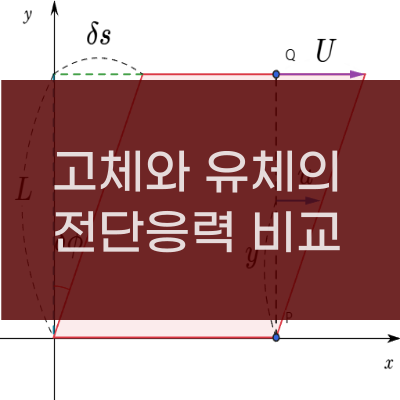
고체와 유체에서 전단변형률, 전단응력과 전단계수, 점성계수에 대해서 알아보자 - 고체의 전단변형률 (shear strain) $ \gamma = \dfrac{\delta s}{L} = tan \delta \phi $ 미소 변형 $( \delta \phi $ \gamma = \dfrac{\delta s}{L} = tan \delta \phi \approx \delta \phi $ 가 된다. - 유체의 전단변형률 $ \delta s = U \cdot \delta t$ ( 이동거리는 속도 x 시간 )이므로, 전단변형률은 아래와 같이 표현 할 수 있다. $ \gamma = \dfrac{\delta s}{L} = \dfrac{U \cdot \delta t}{L} \approx \delta \phi $ ..